The strange row of numbers
Just for fun, a mathematician once made up a puzzle about rabbits. It
went like this.
Suppose that you have a boy rabbit and a girl rabbit. Each month, your
pair of rabbits has a boy rabbit and a girl rabbit. Suppose each pair of
baby rabbits is grown up in just two months. Then they have a pair of
baby rabbits each month. How many rabbits will there be at the end of a
year?
You can figure it out quite easily for a while. First, there are two
rabbits.

By the end of one month, the two rabbits have a pair of baby rabbits. So
now you have four rabbits.
By the end of the second month, the first two rabbits have another pair
of babies. Now there are six rabbits altogether.
In the third month, things begin to get harder to figure out. The first
pair of rabbits have another pair of babies. That makes eight rabbits.
But now the baby rabbits born in the first month are old enough to have
their first pair of babies. So, altogether that makes ten rabbits.
It gets even more complicated during the fourth month. The first rabbits
have another pair of babies, making twelve rabbits. The second pair of
rabbits also has another pair of babies, making fourteen rabbits. And
now the pair of rabbits born in the second month are old enough to have
a pair of babies. That makes a total of sixteen rabbits in the fourth
month.


As you can see, things are now going to get harder and harder to figure
out.
Actually, there’s a way of finding out the answer without counting up
any more pairs of rabbits! It’s hidden in the first five numbers we got
by counting up all the rabbits.
Write the five numbers—2, 4, 6, 10,16—on a piece of paper. Can you
see the secret?
If you add up any two numbers that are next to one another, the sum is
the same as the following number! Add up the first two numbers, 2 and 4,
and you get the third number, 6. Add the second and third numbers, 4 and
6, and you get the fourth number, 10.

And add the third and fourth numbers, 6 and 10, and you get 16, which is
the fifth number!
So you see, you can find out the answer to the rabbit problem simply by
adding up two numbers at a time. Add the last two numbers in the
column—10 and 16—and then put the new number you get at the end of
the column. Then add up the last two numbers you now have. Keep doing
this until you have thirteen numbers in the column.
The first number—2—is the number of rabbits that you started with.
The next twelve numbers—one number for each month of the year—show
how many rabbits you had by

the end of each month. The last number is the number of rabbits at the
end of the year.
A series of numbers of this sort is called a sequence, which means “a
group of things that are connected together.” The mathematician who
worked out the rabbit puzzle discovered a number sequence that goes 0,
1,1, 2, 3, 5, 8, 13, 21, 34, and so on.
As you can see, any two numbers that are next to each other add up to
the next number. Thus 0 and 1 are 1, 1 and 1 are 2, 1 and 2 are 3, and
so on. This sequence is called the Fibonacci sequence (fee buh
[nah]{.smallcaps} chee [see]{.smallcaps} kwuhns), after the man who
discovered it.
Now, there’s something really strange about the Fibonacci sequence.
Nature uses it! The bumps upon a pineapple, the scales on a pine cone,
the leaves on the stem of a rose bush, and the little bumps in the head
of a daisy are all arranged in the Fibonacci sequence!
For example, if you look at a daisy you’ll see that all of the little
yellow bumps make up winding rows called spirals. Some of the spirals go
to the left and some go to the right.
If you count the spirals that go to the left, you’ll see there are 21 of
them. Count the spirals that go to the right and you’ll see there are
34. And the numbers 21 and 34 are next to one another in the Fibonacci
sequence!
If you count the spirals on a pineapple, you’ll find there are 8 going
one way and 13 going another—and 8 and 13 are next to one another in
the Fibonacci sequence. Count the spirals on a pine cone and you’ll get
the numbers 5 and 8, and they, too, are next to one another in the
Fibonacci sequence. It looks as if nature uses mathematics, too!

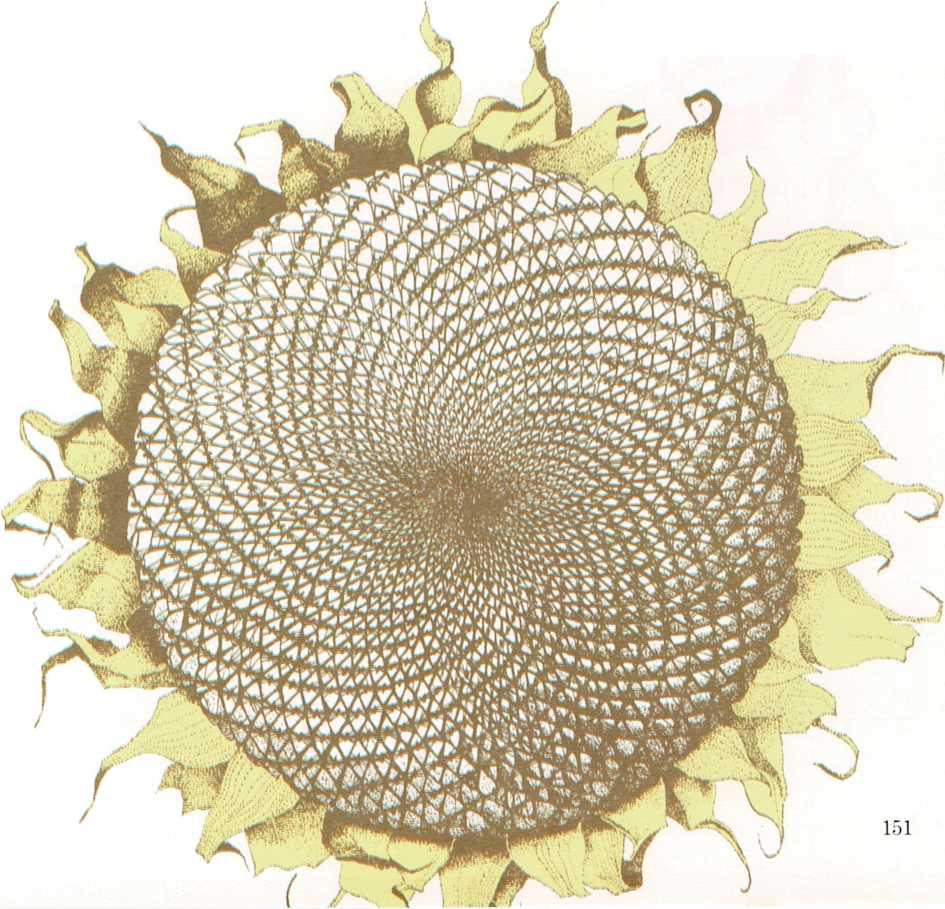
(above) The pattern of spirals shows how the bumps on a giant
sunflower are arranged. There are 34 spirals in one direction and 55
spirals in the other. The numbers 34 and 55 are next to each other in
the Fibonacci sequence.