Counting like a computer
When you see a 1 and 0 together, you would say they stand for ten. But
to a computer, they stand for two!
We count with ten numerals—0, 1, 2, 3, 4, 5, 6, 7, 8, 9. But a
computer uses only two, 1 and 0. So, a computer’s numbers don’t look
like the numbers we are used to seeing. Our eight is 8. But a computer’s
eight is 1000!
This seems strange, but here’s how it works. Our number system has a
base of ten. That is, we group numbers by tens. Ten ones is ten. Ten
tens is a hundred. Ten hundreds is a thousand. And so on. When we write
235, we’re showing that this number is made up of two hundreds, three
tens, and five ones.

Each numeral is like so many beads on an abacus. Its place, or position,
shows how much it stands for.
But a computer doesn’t use a base of ten.
A computer uses a base of two. It doesn’t have places for ones, tens,
hundreds, and so on. A computer has a ones place, a twos place, a fours
place, an eights place, and so on.

When a computer records 2, it does it as 10.
This means “one two and no ones.” It records 4 as 100. This means “one
four, no twos, and no ones”:

Here’s how the numbers from one to ten look when recorded inside a
computer:
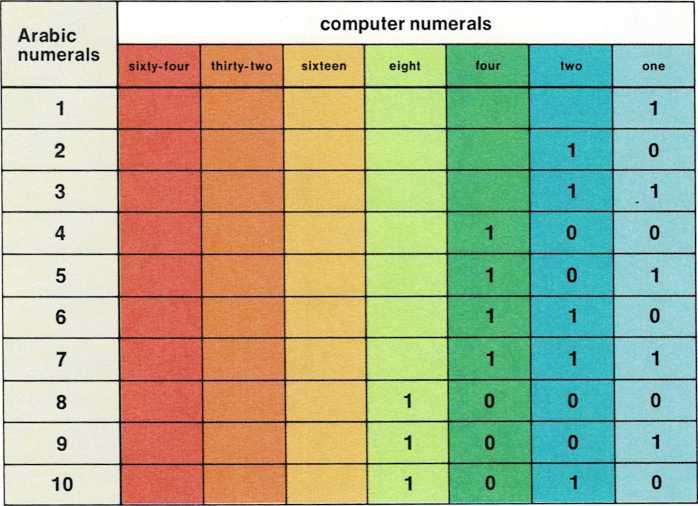
For the number one hundred, we write 100.
A computer records 1100100. Can you see why?
![]()
What this means is 64 + 32 + 4—which comes to 100. As you can see, a
computer simply adds numbers together. But that’s a job a computer is
really good at. It can add up numbers faster than you can blink an eye!

